Propulsion by Propellers Propulsion by PropellersOne of the quite often discussed mysteries among modelers is the selection of an equivalent 3 blade propeller for an existing 2 blade propeller. The following tips should help you in finding a good first start for a multi-blade propeller - some experiments will be necessary to find the "optimum" propeller.
In general each propeller blade needs a certain amount of power to be turned at a certain number of revolutions per minute and a given flight speed. Adding a third blade to a 2 blade propeller would increase the necessary power by 50%. Thus a different propeller diameter has to be selected for the same available power. If a family of propellers is available from a manufacturer, all propellers should have the same basic planform and twist distribution, which makes it possible to select a smaller multi-blade propeller as a replacement for a two bladed propeller.
The propeller pitch is affected only by a negligible fraction, if we do not change to a very high number of blades. It could be reduced by 1 to 5 percent if more than 3 blades are used. Thus we can use the same pitch for the first selection. Therefore we note, that a change of the diameter D while keeping the pitch height H constant will also change the pitch/diameter ratio H/D.
The diameter of a propeller, taken from a family of similar propellers, is
very important for its power consumption. The power needed to turn a propeller
depends directly on the number of blades and on the diameter by a power of 5.
Scaling a propeller so that the diameter is doubled increases the necessary
power to 
.
Changing the number of blades from
to
increases the power consumption
from P1 to
if we use
identical blades (having the same shape, diameter, and pitch).
A scaling of the complete propeller, so that the diameter changes
from 
to
changes the power needed to
turn the propeller at the same number of rotations per minute to
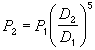
when the number of blades stays the same. Note that the scaling operation also changes the pitch height from H1 to H2 according to the geometric scaling law:
Now, as we want to maintain the revolutions per minute and the forward speed we must also maintain the pitch H of the propeller: H2 = H1. Therefore the ratio H/D changes and we must account for this effect. Test results indicate that the power consumption is almost directly proportional to the ratio H/D. For a given diameter a doubling of the blade pitch results in twice the power consumption:
.
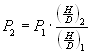Putting both trends together (for propellers of the same power consumption)
and solving for the new propeller diameter
finally leads to the formula
.
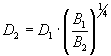Switching from a two bladed to a three bladed propeller corresponds to a new diameter of
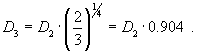
So we could replace a 2 bladed 12 x 10 inch model aircraft propeller by a 10.8 x 10 inch three bladed propeller - if we can find one; the pitch H is 10 inches in both cases.
Switching to a four bladed propeller instead requires a reduced propeller diameter of
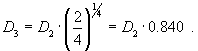
Now the replacement propeller for our 2 bladed 12 x 10 inch model aircraft propeller would be a 10 x 10 inch four bladed propeller.
As a result we can state that a diameter reduction by 10% is necessary for the 2 > 3 blade change and a reduction by 16% for the 2 > 4 blade change.
A set of propellers having approximately the same power consumption.
All these relations are valid only for propellers of the same family having similar blade shapes. You can use the same diameter for different blade numbers if you change the width of the blades. Also the aerodynamic influence of additional blades reduces the power consumption by a small amount, which means, that the replacement 3 blade prop will consume slightly less power than calculated above. On the other hand it will operate at lower Reynolds numbers so that some additional losses can be expected. The formulas shown above should get you close to a working solution, though.
Where do you want to go now?
Propulsion by Propellers 
Design a Prop 
Optimum Propellers
How a Propeller works
Last modification of this page: 21.05.18
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.