For a comparison of engine test results it is common to reprocess the data as if they were taken at standard conditions. These standard conditions are selected arbitrarily and one possible set is listed in table 1 below.

| The performance of an internal combustion engine depends on the amount
of air or, more precisely, the amount of oxygen, which can be burned in
one engine cycle. This amount can be expressed as a function of the
density of air, which is depending on atmospherical conditions. The
density specifies the mass of air, which is contained in a certain volume.
Because the atmosphere is a compressible gas, pressure and temperature
have a strong influence on its density. Additionally, the amount of oxygen
is reduced, when the humidity is increased.
For a comparison of engine test results it is common to reprocess the data as if they were taken at standard conditions. These standard conditions are selected arbitrarily and one possible set is listed in table 1 below. |
 |
We can split the correction into three parts, namely
The correction factors, derived in the following sections, are applied to the actual, measured data to find the equivalent power and rotational speed at standard conditions. Using the inverted factors, we can convert from standard to arbitrary conditions. The correction can be up to 10% of the power, depending on the conditions of the atmosphere.
The density of the air depends directly on the ambient pressure, which leads to a pressure correction of
![]() .
.
The influence of the temperature is similar to the pressure and results in the correction factor
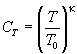 ,
,
where
![]() =
1.4 is the isentropic exponent (ratio of specific heats).
=
1.4 is the isentropic exponent (ratio of specific heats).
For the humidity correction it is necessary to consider the amount of water in the air to derive the mass of air which is available for combustion. Usually, the relative humidity is used to measure the amount of water in the air. The relative humidity is the ratio of the actual mass of water in the air to the maximum possible value, which depends on the temperature. When the maximum is reached, we can observe fog as the excess water starts to drop out of the air. A relative humidity of 100% does not mean, that we are under water; instead, we have vaporized the maximum possible amount of water. Hot air can hold more water than cold air - 50% relative humidity at 0°C means less water in the air that 50% at 30°C (in winter the air is dry, so that some people try to raise the humidity in their rooms artificially). When hot, humid air is cooled down, its relative humidity is increasing until water drops out - this can be observed in refrigerators and air conditioning units.
Using the partial pressure of the water vapor and some thermodynamics leads to the expression
![]() ,
,
where
| is the partial pressure for the current ambient temperature T, (see tables of the properties of steam), | |
| is the relative humidity, | |
| is the partial pressure for the standard conditions. |
If we use a propeller to brake the engine, we have to take into account, that not only the power of the engine depends on atmospherical conditions, but also the power required by the propeller. Recalling the performance coefficient of a propeller:
![]()
we see, that it contains the density of air. Assuming, that the Reynolds numbers are fairly close, the power coefficient for a given propeller will always be the same. Rearranging the equation and setting up the relation between two different atmospherical conditions, we find, that the velocity of rotation depends on the density and the power input. On a hot day, with low pressure, the density of air is smaller than on a standard day, which makes it is easier to turn a propeller at a given speed. The correction factors for the engine power have been derived above, so that we end up with a factor CR, describing the influence of the density of air on the propeller speed:
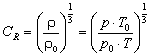 .
.
If we do not use a propeller to brake the engine, we can set this correction factor to 1.0.
When the three correction factors have been calculated, the power for each measured data point has to be multiplied by these factors:
![]() .
.
Also, the rotational velocity has to be corrected. With the aerodynamic characteristics of a propeller, this correction leads to the corrected speed
![]() .
.
| Ambient Temperature | T0 | 288.15 K | 15 °C |
| Ambient Pressure | 100000 Pa | ||
| Relative Humidity | 75 % |
Last modification of this page: 21.05.18
![]()
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.