Wing in Ground Proximity (WIG)

From the beginning, JavaFoil had the basic capability to handle multi-element airfoils. This capability was hidden, though. Based on these foundations it was relatively easy (within a few days)  to add a ground effect simulation. Internally this option works by creating a mirror image of the current airfoil below the ground, which is assumed to be at y=0. This creates a system of multiple airfoils which is symmetrical about the y=0 plane. The flow around this system can be analyzed using the panel method and the usual boundary layer analysis can be performed to calculate the friction drag.

Note: For highest performance, one would implement such  features like ground effect or a cascade option by adapting the calculation of the aerodynamic influence coefficients inside the panel method. Thus one would keep the equation system to be solved at the same size as for a single airfoil. In JavaFoil, the way of actually duplicating the airfoil for the WIG simulation has been chosen. This leads to a more straightforward coding scheme and fits the multi-element option perfectly.

WIG at 0° AOA

a = 0°

 WIG at 5° AOA

a = -5°

 In order to analyze the flow at different angles of attack, the geometry has to be rebuilt for each angle of attack because the geometry of the system must stay symmetrical (see pictures at left). This requires a new panel analysis for each angle of attack, which makes the analysis slower than the plain airfoil analysis. JavaFoil does all this behind the scenes so all you have to do is to toggle the ground effect switch on the Options card.
Angle of attack for a WIG. During the WIG simulation the angle of attack of the airfoil is changed by rotating the airfoil around the point (0.25/0). This point is located on the ground as shown at the left.
Test results for the X-114 WIG aircraft. While the example below shows a downforce application, ground effect can also be used to increase lift without increasing drag excessively. This results in an improved ratio of L/D for lifting applications. Such devices have been employed in vehicles traveling with reduced power over flat surfaces, mainly over water. 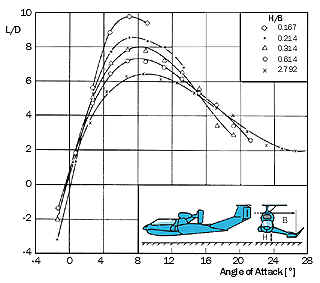Starting in the 1960s, Alexander Lippisch was probably one of the first to exploit this phenomenon in his various ground effect machines. The results of wind tunnel tests for one of his designs (the X-114) are presented at the left. They show an increase in L/D from about 6 to 10 for the complete aircraft (tests were conducted at the German Aerospace Research Center DLR in 1979).

The largest machines of this type were built in the former Soviet Union, though.

 

An Example: Front Wing of a Race Car

The following example shows, how JavaFoil can be used to analyze the effect of ground proximity on the downforce of an airfoil. Such a condition could occur on the front wing of a race car. As this is only a simple example, the results should not be taken as general. It is clear that an airfoil must be designed and optimized to work efficiently in ground effect. If you want to use this feature in JavaFoil, it is recommended to plan exactly what you want to analyze and which steps you have to perform in order.

Geometry Card
  • Create a NACA 4412 airfoil section with negative camber (-4%).
  • JavaFoil will create the name "NACA -4412" as the camber is negative.
  • Alternatively, you could also create a positively cambered section and "Flip" it in y-direction on the Modify card.
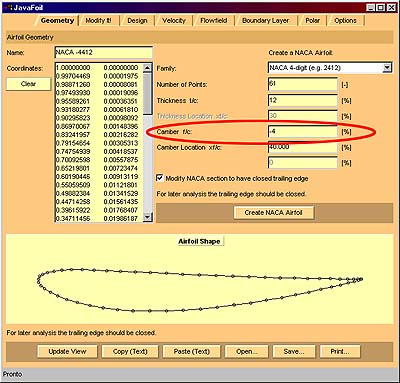 Creating an airfoil with negative camber

Modify Card
  • Rotate the airfoil by -10° for a more realistic setup.
    Note: the current geometry always represents an angle of attack of 0° as the rotation of the airfoil has become part of the geometry.
  • Translate the airfoil upwards by 20% of its chord. The 25% chord point of the airfoil is now located at the point (0.25/0.20). This creates the required free space between airfoil and ground (which is always at y=0).
  • Make sure that there is no intersection with the ground.
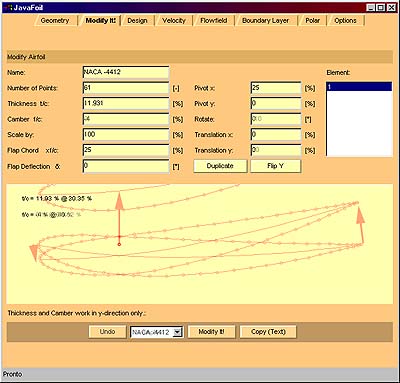 Modifying the airfoil location and orientation.

Flow Field Card
  • Perform flow field analysis without ground effect for comparison.
  • You can analyze the flow at different angles of attack - see remark about the 0° angle above (Modify card).

Note: for "free flight", the y=0 axis is always located at the center of the graph.

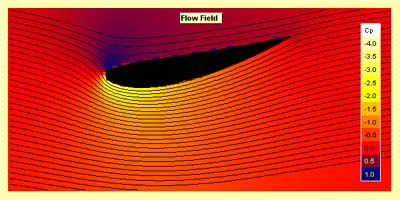 The flow field without ground effect.

Options Card
  • Check the "ground effect" option. This activates the simulation of a flat floor, located at y = 0 (this is why we have moved the airfoil upwards by 20% of its chord).
 Activating the ground effect option.

Flow Field Card
  • Perform another flow field analysis with ground effect.
  • The picture clearly shows the low pressure field (high velocity) between the lower surface and the ground.
  • Again, you can analyze the flow at different angles of attack.

Note: with ground effect activated, the y=0 axis is always located at the lower edge of the graph.

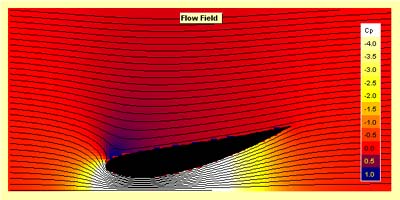 The flow field with ground effect.

Velocity Distribution Card
  • You can compare the velocity distribution for any angle of attack without and with ground in effect.
  • The picture clearly shows the high velocity level on the lower surface in presence of the ground (square symbols). The steep velocity drop towards the trailing edge (pressure rise)  may lead to separation and increased drag.
  • On the upper surface (lower curves), a small difference occurs mainly at the leading edge, as the stagnation point is shifted downstream by the ground effect.
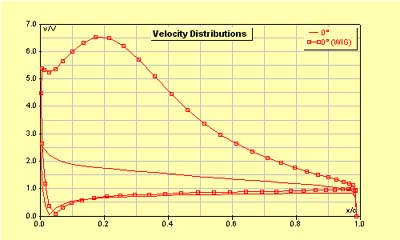 The velocity distribution with and without ground effect.

Polar Card
  • To check the airfoil for different angles of attack, you can analyze an complete polar for different angles of attack and Reynolds numbers. The angle of attack is changed by rotating the airfoil around the point (0.25/0), which will change the height of the airfoils 25% chord point above ground somewhat.
  • The comparison shows that the downforce increases from CL = -1.7 for the free airfoil to -5.7 due to the ground effect!
  • It is also clearly visible that in our example the drag coefficient increased largely, though. L/D went down from about 100 for the free flow field to 60 due to the presence of the ground.
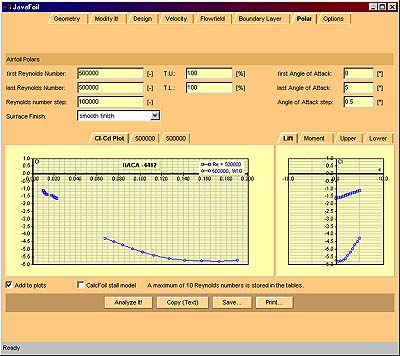 Comparison of the polars with and without ground effect.

Critical Issues:

Last modification of this page: 21.05.18

[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.

Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.

It might take some time until you receive an answer and in some cases you may even receive no answer at all. I apologize for this, but my spare time is limited. If you have not lost patience, you might want to send me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose. Any statements may be incorrect and unsuitable for practical usage. I cannot take any responsibility for actions you perform based on data, assumptions, calculations etc. taken from this web page.

© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this document for a publication, you have to cite the source. A publication of a recompilation of the given material is not allowed, if the resulting product is sold for more than the production costs.

This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.

This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.

Impressum       Datenschutz